Applications of the MDL Principle to Prediction and Model Selection and Testing

• Duration: 1.1.2009 – 31.12.2012
• Funding: Academy of Finland
• Project leader: Professor Petri Myllymäki
• Keywords: MDL, normalized maximum likelihood, universal models, variable order Markov chains, model selection, model testing

Abstract

The main application areas of statistical inference are model selection, hypothesis testing, and prediction. In model selection the goal typically is to increase our understanding of a problem area, by utilization of data analysis, data mining, and information extraction tools, and in hypothesis testing we estimate the validity of a certain hypothesis about the problem. In prediction, the task, of course, is to estimate the probability of some unknown quantity, which typically is temporally located in the future. To perform these statistical inference/machine learning tasks we need a theoretically solid framework, which is logically correct satisfying certain reasonable optimality criteria, while at the same time providing computationally feasible methods for practical applications. Information theory offers an excellent foundation for such a framework.

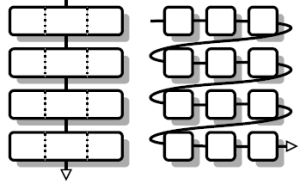Fig. 1. Illustration of different normalization methods in universal models: a) sequential normalization (left), and b) factorized sequential normalization (right). Source: [2].

Our earlier pioneering work on information-theoretic statistical inference, in which the Minimum Description Length (MDL) principle plays a central role, has recently spurred an influx of new ideas, problems, and extensions. We believe that the new ideas lead to theoretically and practically significant advances in MDL-based modeling. The goal of the project is to study these issues further, focusing on four research areas: sequentially normalized universal models, optimally distinguishable models, extensions of the structure function, and non-stationary modeling. In addition to theoretical advances in these areas, we will develop new algorithms suitable for practical model selection, testing, and prediction tasks, and empirically demonstrate their validity using both artificial and real-world data sets from various domains.

Publications

1. J. Rissanen, Model Selection and Testing by the MDL Principle. Chapter 2 in F. Emmert-Streib and M. Dehmer, eds., Information Theory and Statistical Learning, Springer, 2009.
2. T. Silander, T. Roos, and P. Myllymäki, Locally Minimax Optimal Predictive Modeling with Bayesian Networks. To appear in Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS 2009), Clearwater Beach, FL, USA.
3. T. Roos and B. Yu, Sparse Markov Source Estimation via Transformed Lasso, IEEE Information Theory Workshop (ITW-09), Volos, Greece, June 10–12, 2009.
4. T. Roos and B. Yu, Estimating Sparse Models from Multivariate Discrete Data via Transformed Lasso, Information Theory and Applications Workshop (ITA-09), San Diego CA, USA, February 8–13, 2009.
5. T. Roos, P. Myllymäki, and J. Rissanen, MDL Denoising Revisited, IEEE Trans. Signal Processing, 57:9, 3347–3360, 2009.
6. T. Silander, T. Roos, and P. Myllymäki, Learning locally minimax optimal Bayesian networks, International Journal of Approximate Reasoning (Special Issue on Selected Papers from PGM-08), 51:5, 544–557, 2010.
7. J. Rissanen, T. Roos, and P. Myllymäki, Model Selection by Sequentially Normalized Least Squares, Journal of Multivariate Analysis, 101:4, 839–849, 2010.
8. J. Rissanen and P. Myllymäki, MDL Interval Estimation, Information Theory and Applications Workshop (ITA-10), San Diego, CA, USA, February 1–5, 2010.
9. J. Rissanen, The MDL Principle, in C. Sammut and G.I. Webb (editors), Encyclopedia of Machine Learning, Springer, 2010.
10. D.F. Schmidt and T. Roos, On the consistency of sequentially normalized least squares, to appear in Proc. 3rd Workshop on Information Theoretic Methods in Science and Engineering (WITMSE-10), 2010.
11. A. Carvalho, T. Roos, A. Oliveira, and P. Myllymäki, (2011). Discriminative learning of Bayesian networks via factorized conditional log-likelihood, Journal of Machine Learning Research 12(Jul):2181–2210.